度量程序架构
第一次作业
架构解说
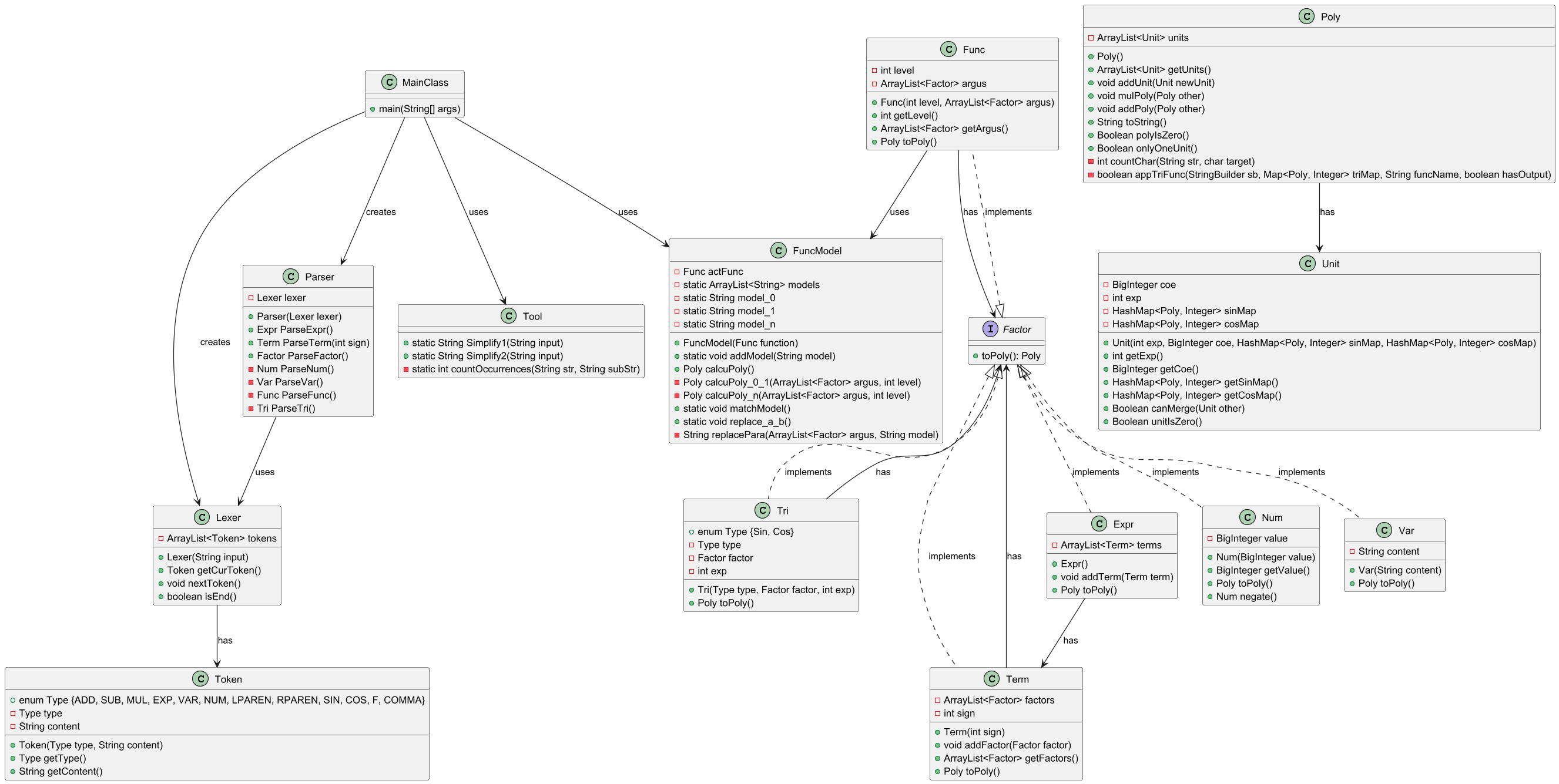
第一次作业中,我将所有类分为了主类MainClass和4个包,如下
Expression:管理解析表达式时生成的Expr、Term和Factor实例,其中Num、Var和Expr类实现了Factor接口。这样做的好处是不用另开“子表达式”这一类。另外,我的Term类中有一个属性为Sign,它表示在表达式中每项的正负号,这样表达式在解析项时返回的项就完全包含了这个项的全部信息,递归下降就能发挥出威力,
LexerAndParser:管理词法分析器Lexer类、语法分析器Parser类,是递归下降分析表达式层次的主要工具
PolyandUnit:管理和运算生成的多项式,其中Poly类包含多项式相加、相乘和toString方法。值得一提的是,第一次作业我没有构建Unit类,而是在Poly类中直接用一个Hashmap<指数,系数>存所有的因子,由于第一次作业只有变量因子可以这么做,迭代后显然不行了。
Tool:管理工具类,目前负责化简输入的表达式使其能够被解析
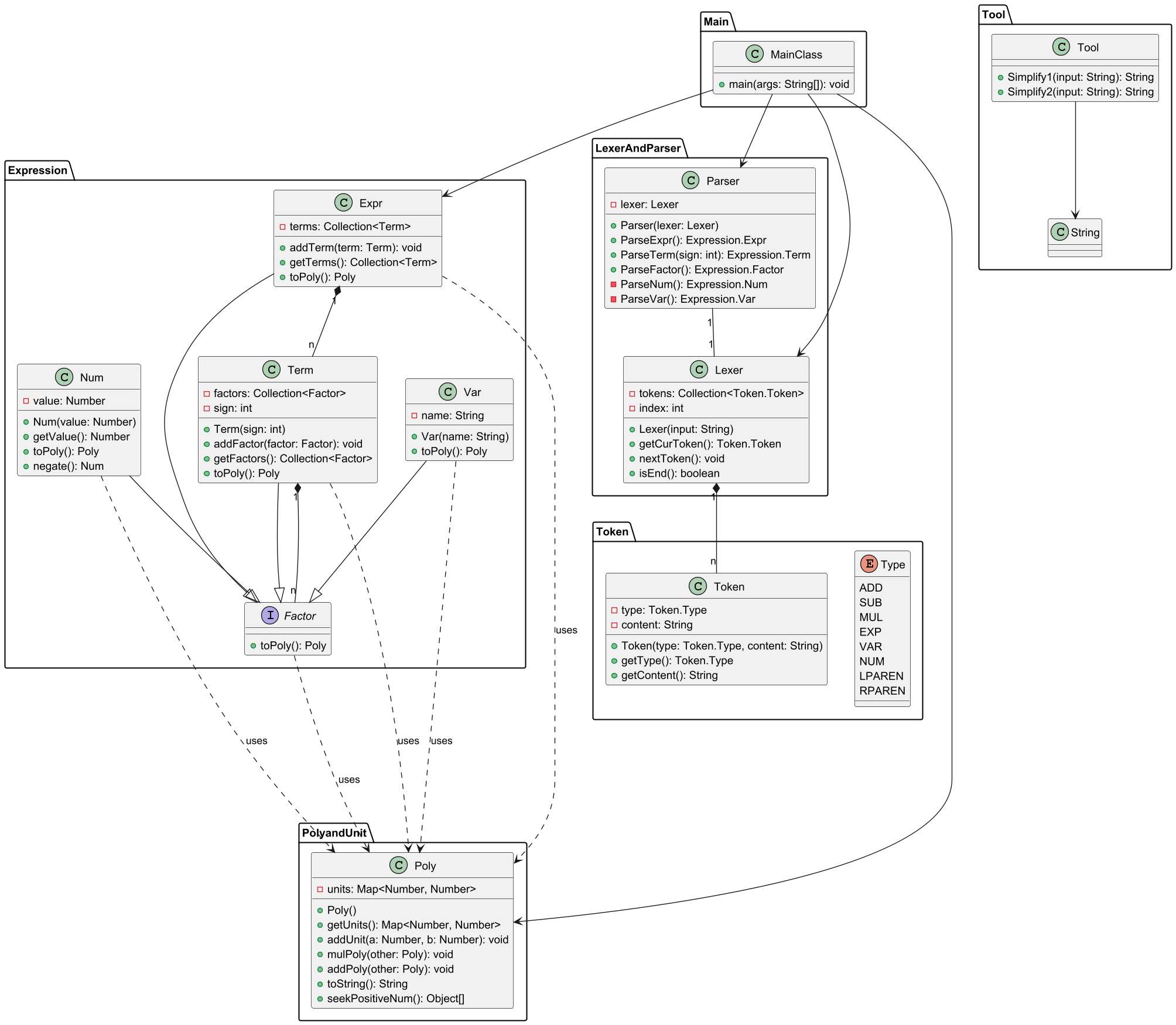
复杂度分析
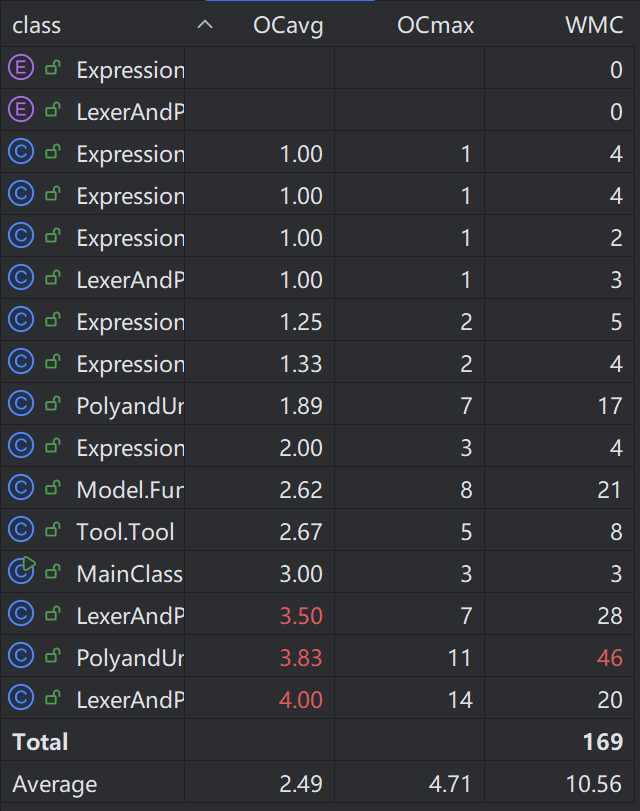
可以看到Parser、Lexer和Poly类的复杂度远高于其它类,我认为主要原因是Parser和Lexer两类高度耦合,在Parser类中大量调用Lexer类的方法,并且两个类本身就具有比较高的复杂度。而Poly类中有较多对于多项式运算的方法(包括一个优化方法)以及toString方法,因此复杂度高也是正常的。
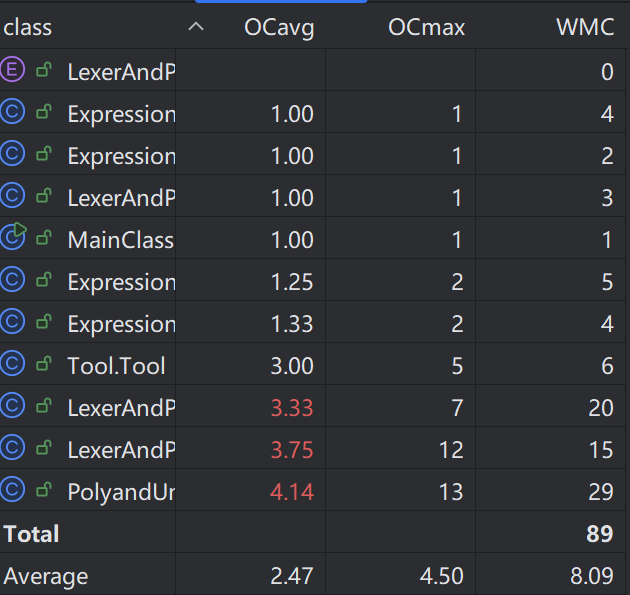
由于我比较注重封装的意识,因此写了不少方法。除了Poly类的toString和seekPositiveNum方法以外,都比较简单。关于这两个方法为什么如此复杂,实际上是我在第一次作业中走的一些弯路。比如toString方法中大量嵌套了分支结构,事实上只需要考虑单项式各个部分在什么情况下需要输出,seekPositiveNum方法可以被给单项式降序排序的方法替代。
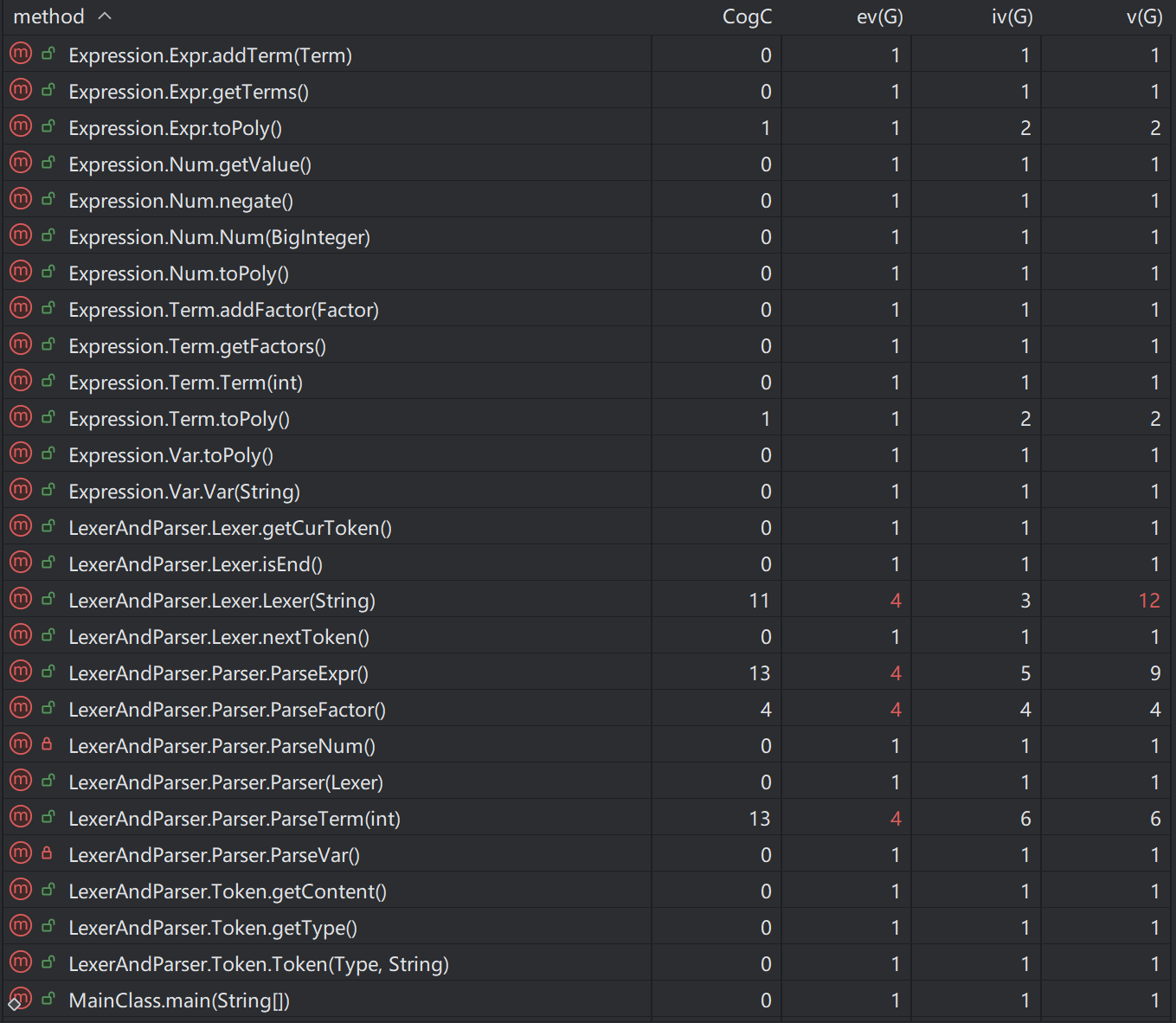
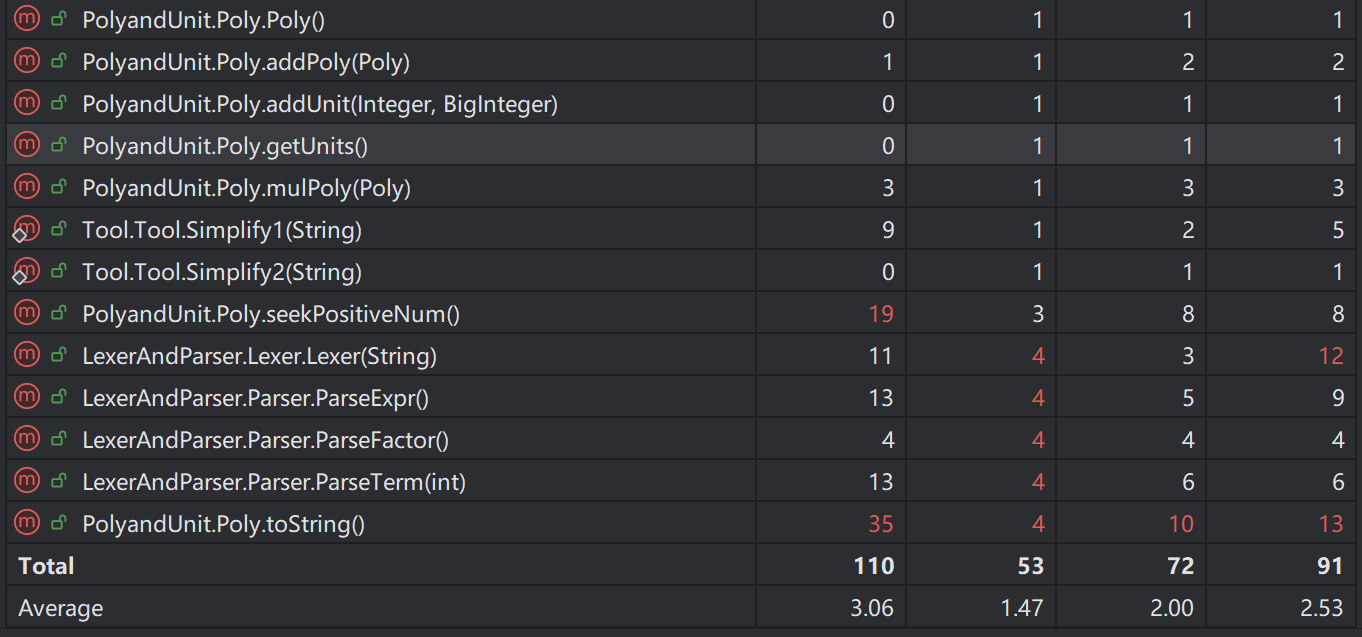
第二次作业
架构解说
正如前面所说,在加入了三角函数因子后,我不得不构造了Unit类用来代表一个单项式,并且修改了相关逻辑。由于现在的单项式比较复杂,可能含有三角函数,因此我的Unit类包含4个属性,能够唯一确定一个单项式:
private BigInteger coe; // 系数
private int exp; // x的指数
private HashMap<Poly,Integer> sinMap; // sin函数集合<内部多项式,指数>
private HashMap<Poly,Integer> cosMap; // cos函数集合<内部多项式,指数>
此外,我还另开了一个三角函数类Tri来代表三角函数因子,有两个枚举类型,分别是sin和cos,代表两种三角函数
Tri类属性如下:
private final Type type; // 三角函数类型
private Factor factor; // 函数内的因子
private int exp; // 三角函数的指数
Func类代表递推函数因子,FuncModel管理递推函数的模式,并且实现递推函数的计算(因为只会有一种递推函数)
关于递推函数->多项式的计算,我采用了实参字符串替换+递归求递推函数的办法。尽管指导书中说明了n不会超过5,但是这样有比较好的扩展性,能达到“一劳永逸”的效果。这里有两处细节:
- 在替换字符串时,要提前将“函数模式”中的形参x,y换成其它的字母。否则,如果出现f(y,x)的情况:当我们用第一个实参替换掉y,准备替换x时,会将字符串中所有的x都替换成第二个实参,造成错误。这一工作我在一开始读到3行“函数模式”后就进行了
- 对于序号为0、1和序号大于1的函数要区别对待。前者直接替换实参,后者要替换实参+替换函数序号+进入递归,递归的边界条件就是函数序号为0或1。这部分的递归比较简单,只需要写好对序号为0、1的函数的处理即可。
前一次作业Poly类的toString方法写的笨拙且臃肿,加入三角函数以后我不可能再在原来的代码块上添加,否则就会超出60行的限制,在借助了AI工具后我很好地将它变得逻辑清晰,大大减少了分支数量和代码量。其原因在于我一开始是将一个Unit看成一个整体,而前面已经提到Unit有4个属性,这就导致要不停地考虑每个属性对应的多种情况,其分支多达十几种。化简后的代码独立考虑四个属性分别怎么输出,逻辑上简便了不少。
在这次作业中令我印象深刻的是封装了两个判断单项式和多项式是否为0的方法。在判断单项式是否为0时不得不判断三角函数中是否有0,而三角函数中又有多项式,需要挨个判断里面的单项式是否为0。这里再次用到了递归的思想,方法写成后非常成功。
复杂度分析
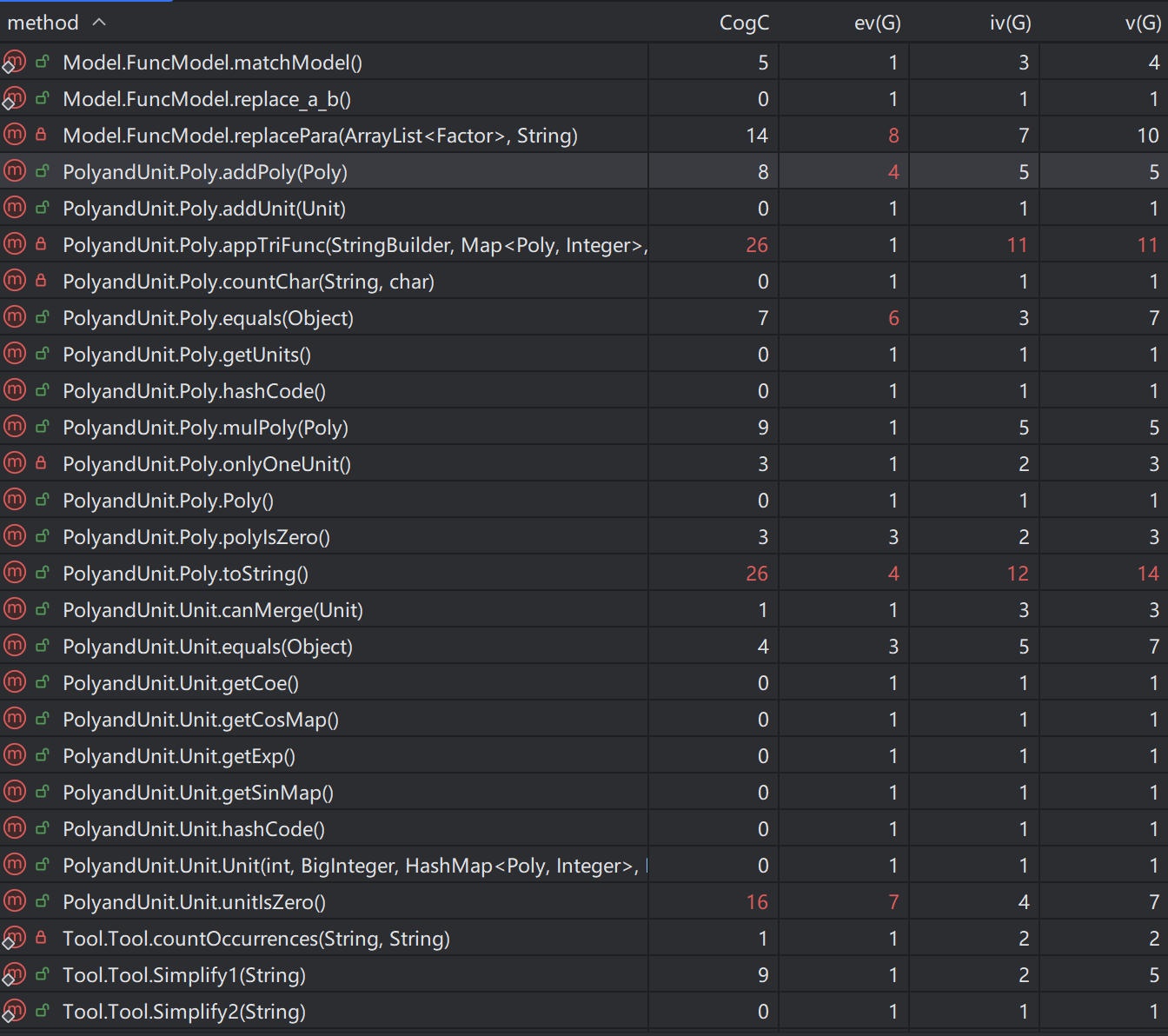
可以看到,由于toString方法在逻辑上的大大简化,在加入了三角函数方法后,Poly类的复杂度甚至比之前还要低!而剩下两个类的复杂度和之前相比只有略微提升,这是正常的。
可以清楚地看到,这次的toString方法复杂度由35降到了26,说明分支机构的嵌套确实会大大增加复杂度。
unitIsZero这个方法就是用来判断单项式是否为0的,因为有递归的存在导致复杂度较高。
appTriFunc方法封装了三角函数的toString,其逻辑本身就比较复杂,有几层分支嵌套,我还考虑了优化cos(-x),我认为这块代码已经无法再简化,因此第三次作业也一直沿用
第三次作业
架构解说
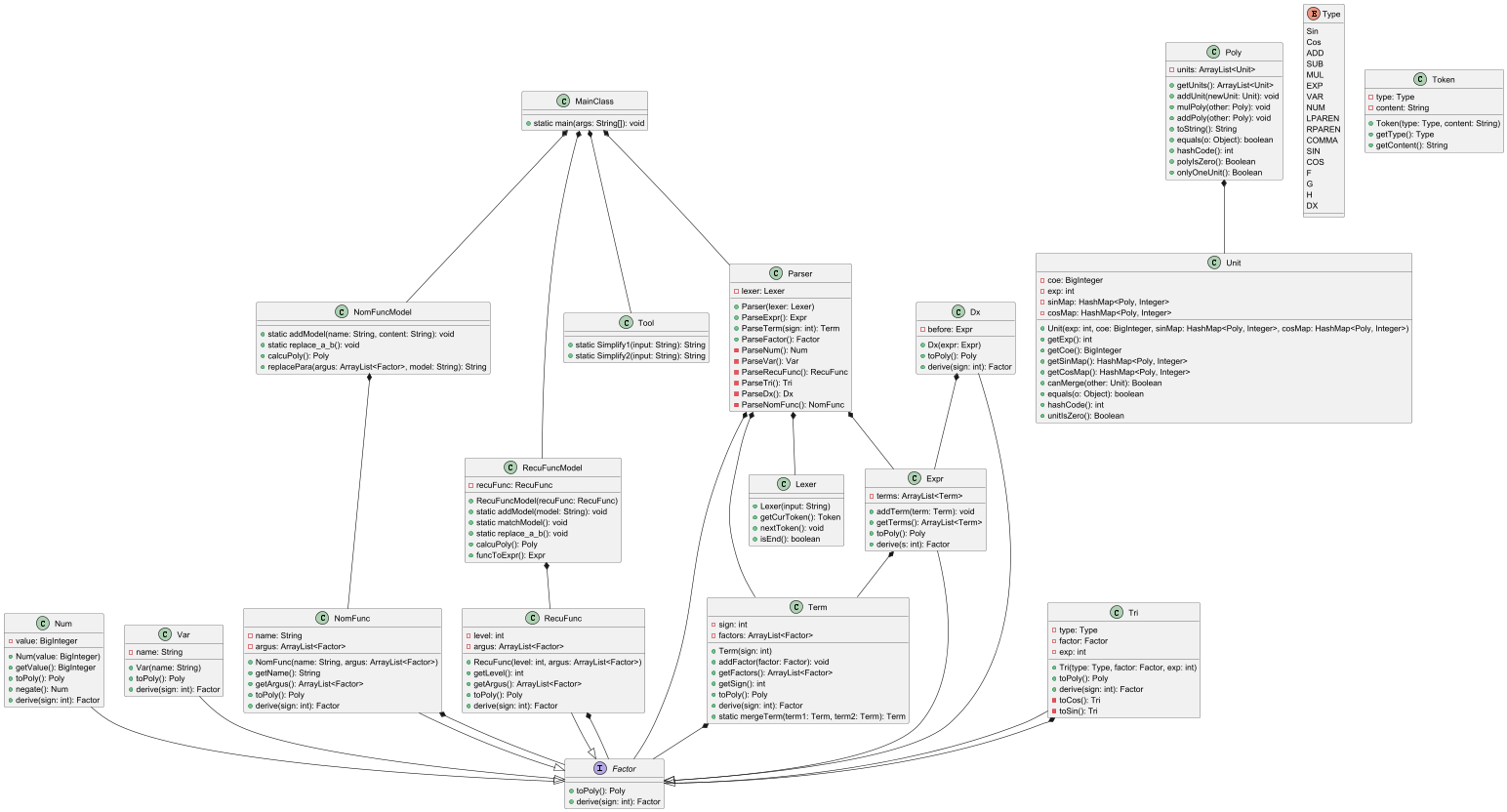
第三次作业和第二次作业相比,架构几乎没有变化,只是增加了一些类和对应的方法。
我为求导因子增加了Dx类,,为自定义普通函数增加了NomFuncModel和NomFuncModel类,功能和递推函数类似
对于求导的解析,我受到课上作业的启发,只需要对各种各样的因子都分别写好求导方法即可。
值得一提的是,我沿用了课上作业的求导方法,即:除了Term类求导返回Expr类型,其它类求导均返回Term类型,这样做的原因是:我的Term类是自带正负号的,三角函数因子求导后符号可能会改变,这样才能将符号的改变正确地传递出来。
复杂度分析
下表均为对最终程序架构的度量
| 类名 | 属性个数 | 方法个数 | 平均圈复杂度 | 最大圈复杂度 | 方法权重和 | 规模(总代码行数) |
|---|---|---|---|---|---|---|
| Dx | 1 | 3 | 1 | 1 | 3 | 20 |
| Expr | 1 | 4 | 1.75 | 3 | 7 | 40 |
| Lexer | 4 | 9 | 3.4 | 10 | 34 | 142 |
| MainClass | 0 | 1 | 4 | 4 | 4 | 44 |
| NomFunc | 2 | 5 | 1 | 1 | 5 | 30 |
| NomFuncModel | 2 | 5 | 2.3 | 8 | 14 | 70 |
| Num | 1 | 5 | 1 | 1 | 5 | 35 |
| Parser | 1 | 10 | 3.5 | 8 | 35 | 191 |
| Poly | 1 | 11 | 4.1 | 11 | 45 | 239 |
| RecuFunc | 2 | 5 | 1 | 1 | 5 | 33 |
| RecuFuncModel | 5 | 6 | 2.5 | 8 | 27 | 202 |
| Term | 2 | 7 | 2 | 4 | 14 | 78 |
| Token | 2 | 3 | 1 | 1 | 3 | 27 |
| Tool | 0 | 2 | 3 | 5 | 6 | 47 |
| Tri | 3 | 5 | 1.6 | 3 | 8 | 65 |
| Unit | 4 | 9 | 1.9 | 7 | 17 | 92 |
| Var | 1 | 3 | 1 | 1 | 3 | 27 |
| 类名 | 方法名 | 方法规模(行数) | 控制分支数目 |
|---|---|---|---|
| RecuFuncModel | calcuPoly | 11 | 2 |
| RecuFuncModel | calcuPoly_0_1 | 17 | 2 |
| RecuFuncModel | calcuPoly_n | 35 | 2 |
| RecuFuncModel | matchModel | 11 | 2 |
| RecuFuncModel | replace_a_b | 8 | 0 |
| RecuFuncModel | replacePara | 25 | 2 |
| RecuFuncModel | funcToExpr | 11 | 2 |
| RecuFuncModel | funcToExpr_0_1 | 17 | 2 |
| RecuFuncModel | funcToExpr_n | 35 | 2 |
| Poly | mulPoly | 42 | 0 |
| Poly | addPoly | 32 | 2 |
| Poly | toString | 58 | 6 |
| Poly | appTriFunc | 29 | 4 |
| Poly | equals | 16 | 3 |
| Poly | hashCode | 1 | 0 |
| Poly | polyIsZero | 10 | 1 |
| Poly | countChar | 3 | 0 |
| Poly | onlyOneUnit | 7 | 1 |
| Poly | getUnits | 3 | 0 |
| Poly | addUnit | 3 | 0 |
| RecuFunc | 构造函数 | 4 | 0 |
| RecuFunc | getLevel | 3 | 0 |
| RecuFunc | getArgus | 3 | 0 |
| RecuFunc | toPoly | 3 | 0 |
| RecuFunc | derive | 3 | 0 |
| Num | 构造函数 | 3 | 0 |
| Num | getValue | 3 | 0 |
| Num | toPoly | 4 | 0 |
| Num | negate | 2 | 0 |
| Num | derive | 2 | 0 |
| Lexer | 构造函数 | 3 | 0 |
| Lexer | LexerBuild | 13 | 3 |
| Lexer | addNum | 10 | 1 |
| Lexer | addSign | 13 | 7 |
| Lexer | addTri | 6 | 1 |
| Lexer | addFunc | 11 | 3 |
| Lexer | addDx | 2 | 0 |
| Lexer | getCurToken | 3 | 0 |
| Lexer | nextToken | 2 | 0 |
| Lexer | isEnd | 2 | 0 |
| NomFunc | 构造函数 | 3 | 0 |
| NomFunc | getName | 3 | 0 |
| NomFunc | getArgus | 3 | 0 |
| NomFunc | toPoly | 5 | 0 |
| NomFunc | derive | 3 | 0 |
| NomFuncModel | 构造函数 | 3 | 0 |
| NomFuncModel | addModel | 3 | 0 |
| NomFuncModel | replace_a_b | 6 | 0 |
| NomFuncModel | calcuPoly | 5 | 0 |
| NomFuncModel | funcToExpr | 5 | 0 |
| NomFuncModel | replacePara | 25 | 2 |
| Term | 构造函数 | 2 | 0 |
| Term | getSign | 3 | 0 |
| Term | addFactor | 2 | 0 |
| Term | getFactors | 2 | 0 |
| Term | toPoly | 10 | 0 |
| Term | mergeTerm | 13 | 2 |
| Term | derive | 14 | 1 |
| Expr | addTerm | 2 | 0 |
| Expr | getTerms | 2 | 0 |
| Expr | toPoly | 5 | 0 |
| Expr | derive | 10 | 1 |
| Tri | 构造函数 | 3 | 0 |
| Tri | toCos | 2 | 0 |
| Tri | toSin | 2 | 0 |
| Tri | toPoly | 14 | 2 |
| Tri | derive | 9 | 1 |
设想新的迭代场景
假设新的迭代场景是加入求多阶导数因子dx{n}(表达式)
则我的Dx类要添加属性:“序号”,来说明该求导因子求的是几阶导。
而所有因子类的derive()方法都要加入新的参数“序号”,来标明要求几阶导。derive()函数内部要通过循环来返回相应阶数的求导结果
bug分析
我自己的bug
第二次作业出现的两个bug均是因为我在lexer类分支复制粘贴时忘记修改相应token了,没有技术含量可言。
第三次作业出现的两处bug均是与求导有关:
- 忽略了求导时的符号问题,所有类的derive()方法都没有传入符号,默认求导得到的都是正项,事实上对Term求导时得到的是表达式因子,其中的子Term的符号需要与父Term保持一致。修复bug时给所有derive()方法补充了sign参数,同时将该参数填入正确的位置
- 忽略了对求导因子求导(嵌套)的问题,
Dx类中没有写对本类实例求导的方法,导致对于dx(dx(x))这样的因子只进行了一次求导
由于bug是因为逻辑不完整导致的,所以修复bug前后的代码圈复杂度没有区别。如果想要降低方法的复杂度,我认为应该多封装方法,少写分支嵌套,这样会减小圈复杂度。
在互测中发现的bug
在互测中我发现了一些比较有代表性的bug,其中大部分都与优化有关。因为A组的同学在正确性上的得分较高,所以我在互测会比较偏向优化hack。同时,这样的判断也源于我观察同学们的代码后可以清晰地看到他们进行了哪些优化。事实上,有些同学的优化方法名写的通俗易懂,这在一定程度上给我构造样例也提供了方向。
- 关于
sin(0)和cos(0)的问题,一部分同学没有直接把sin(0)存成0,或者是最后的toString方法分支判断有疏漏,导致sin(sin(0)^0)这样的样例输出为0 - 关于
sin(x)^2+cos(x)^2的问题,一部分同学没有完全检验三角函数内部的因子是否完全相同,或是三角函数以外的部分是否完全相同,导致错误优化 - 关于
cos(因子)的问题,一些同学优化了内部为负号开头的单项式的余弦函数,但是忽略了要加一层括号,比如:cos((-3*x))应该变成cos((3*x))而不是cos(3*x)。事实上,内部的因子在去掉开头的负号后只要还含有* + -都需要带括号
由于第三次作业被hack的很惨,我发现了构造hack数据的一些技巧。以我自己为例子,我的求导因子有较大的问题,所以当其它同学发现后是由浅入深hack我的:
dx(0):常数因子求导
dx(x^3):变量因子求导
dx(sin(x)) dx(cos(x)):三角函数因子求导
dx((sin(x)+x^3+4)^2):表达式因子求导
dx(-x^3) dx(-sin(x)) :外层负项求导
dx(sin(-x)):内层负项求导
dx(sin((sin(x)+x+1)):嵌套求导
所以以后在构造测试样例的时候也可以这样层层递进地进行,有时能够构造出一些评测机不容易构造的样例
优化分析
我做了对负项不放在开头、sin(0)和cos(0)的优化、余弦函数偶函数性质的优化、以及sin(x)^2+cos(x)^2的优化
负项尽可能不放在开头:在toPoly后将单项式按系数降序排序即可
sin(0):在最后输出之前判断单项式是否为0即可,已经被封装进入方法。
cos(0):在余弦函数toPoly方法中直接将它存成常量1
余弦函数偶函数性质:判断内部是否是单项式且第一项为负号
sin(x)^2+cos(x)^2:三层遍历,找到匹配的内容就合并放入新容器
我的优化可以保证代码的简洁性和正确性,因为我将大块的优化方法封装进了工具类,小块的优化方法也放入了各自的类,需要时调用即可。没有必要封装成方法的用注释说明这部分功能。
心得体会
Unit1给我的感觉属于不轻松也不算难,因为有大量的往届博客可以借鉴,所以在架构选择和递归下降算法上并不困难,但是到具体细节的实现上还是挺繁琐的。第一次作业之前我还反复看了上学期OOpre最后一次作业的递归下降解说,但是直到看完博客之后才完全理解这一算法的妙处。
第一次作业我几乎花了4天的时间才完成,第二次和第三次都是两天多一点,感觉是有些极限了,尤其是第二次作业,周六下午才完全通过。不过不管我在写代码时有多么极限,最终总能成功地在ddl之前通过中测。感觉以后最好周二就开始着手写代码,否则会来不及。
此外,感觉我对面向对象的思想理解更深刻了。在面向对象设计与构造中,一切方法几乎都是要依靠对象而存在(除了静态方法),而在写作业的过程中,常常是一上来先建一个类。这就意味着我们要事先想好每个类代表的到底是什么,因为类是实例的抽象,所以它需要高度概括我所需要的实例的特性。
最后,我很感谢课程组、各位助教的辛苦编写指导书和答疑。第一单元的三次作业难度安排也非常合理,通过解析表达式的过程让我们深刻理解了递归下降法的实际应用。
未来方向
- 可以尝试创新题目,加入更多实际应用的色彩,这样在解决问题的过程中会有更多的乐趣
- 迭代难度适当均衡,避免某一次迭代太难或者太简单的情况
