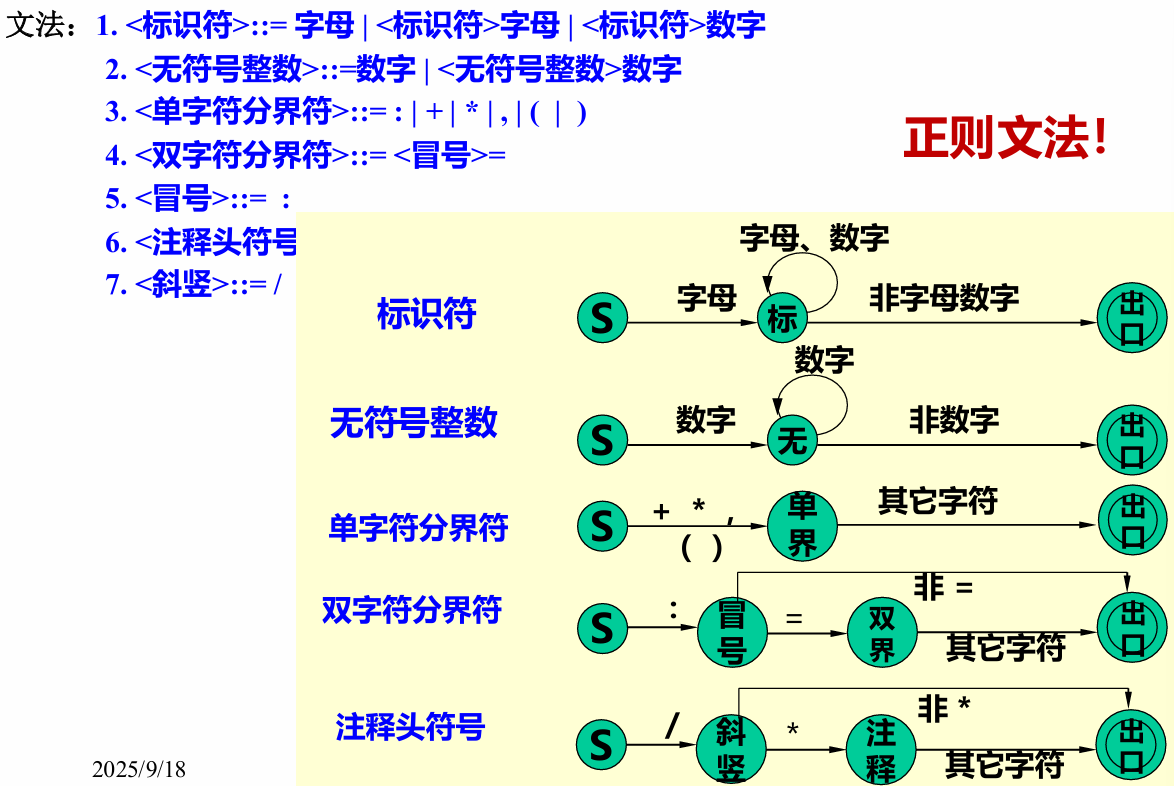
文法
规范推导=最右推导
句型:由识别符号经过0次或多次推导得到,成分随意。一切东西都是句型
句子:由识别符号经过1次或多次推导得到,且完全由终结符构成
语言:所有句子的集合
短语:句型中,可以由前面句型中的某个非终结符通过1次或多次所能推出的符号串。短语必须得是前面某个非终结符推出的完整符号串,而不能是其一部分
e.g.
文法G[<无符号整数>],w = <数字串>1是该文法的句型
<无符号整数> => <数字串> => <数字串><数字> => <数字串>1
在这个例子中,<数字串>不是短语,因为前面的<数字串>推导出的完整符号串是<数字串>1
简单短语:句型中,能由前面某个非终结符一步推导得到的符号串
句柄:最左简单短语
左递归的消除
左递归文法有一个左递归产生式,一个非左递归产生式
左递归产生式本质上是说在符号串右侧可以无限地添加某些成分,非左递归产生式则说明了符号串最左侧必须是某些成分
消除左递归的思想非常简单:左递归和右递归都可以创造无限的符号串,只需要将最左侧的成分单独提取出来,无限符号串的部分可以用一个右递归来代替
e.g.
A -> Ab | a A的最左侧必须是a,后面可以无限添加b,转换成
A -> aB
B -> aB | ε
语法树
如果不在边上标序号,那么语法树实际上失去了推导时的顺序信息。
使用语法树找短语:若某子树的末端结点按自左向右顺序为句型中的符号串,则该符号串为该句型的相对于该子树根的短语
简单短语:找到短语后,其中通过该子树一次推导就能得到的就是简单短语
句柄:语法树最左侧的简单短语
语法树与二义性
若对于一个文法的某一句子存在两棵不同的语法树, 则该文法是二义性文法,否则是无二义性文法。
对于无二义性文法,因为语法树不包含顺序信息,无论用什么顺序推导,语法树都是相同的。即,无二义性文法只有一棵语法树
词法分析
状态图
左线性文法:::=右侧的非终结符一定在左边
换言之,非终结符可以在右侧添加某些终结符。这符合我们读句型时从左到右的习惯,状态图应运而生
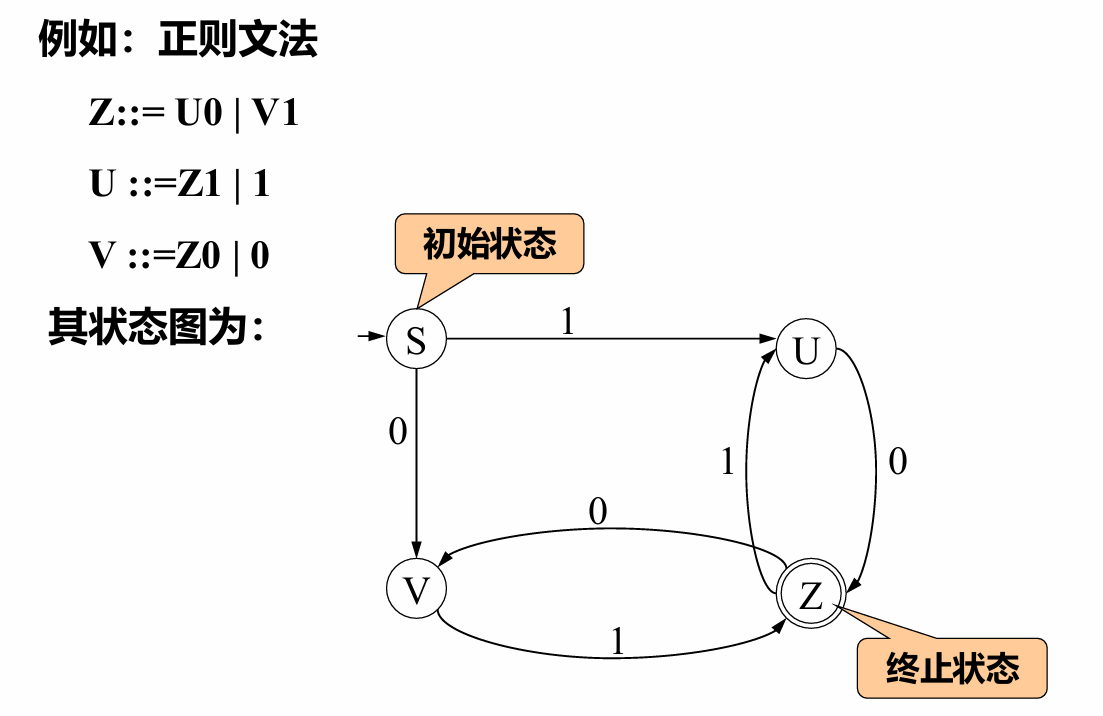
顶层状态就是终止状态
识别一个字符串是否是句子:

上图可以由下面这句话概括:状态图和推导为互逆过程,如果一个字符串不能回到终止状态,说明它不能由开始符号推导得到,则它不是句子
程序设计
由状态图的思想,我们可以设计词法分析程序: